The `bbob` Test Suite

This is an online-friendly presentation of the bbob functions, based on the BBOB 2009 function document (Finck et al. 2009). You may cite this work in a scientific context using

@techreport{bbob2019,
    author = {Finck, Steffen and Hansen, Nikolaus and Ros, Raymond and Auger, Anne},
    title = {Real-Parameter Black-Box Optimization Benchmarking 2009: Noiseless Functions Definitions},
    institution = {INRIA},
    year = {2009},
    number = {RR-6829},
    note = {Updated version as of February 2019},
    url = {https://inria.hal.science/inria-00362633v2/document}
}

We present here 24 noise-free real-parameter single-objective benchmark functions (see (Hansen et al. 2009, 2016) for our experimental setup and (Hansen et al. 2022) for our performance assessment methodology). Our intention behind the selection of benchmark functions was to evaluate the performance of algorithms with regard to typical difficulties which we believe occur in continuous domain search. We hope that the function collection reflects, at least to a certain extend and with a few exceptions, a more difficult portion of the problem distribution that will be seen in practice (easy functions are evidently of lesser interest).

We prefer benchmark functions that are comprehensible such that algorithm behaviors can be understood in the topological context. In this way, a desired search behavior can be pictured and deficiencies of algorithms can be profoundly analyzed. Last but not least, this can eventually lead to a systematic improvement of algorithms.

All benchmark functions are scalable with the dimension. Most functions have no specific value of their optimal solution (they are randomly shifted in x-space). All functions have an artificially chosen optimal function value (they are randomly shifted in f-space). Consequently, for each function different instances can be generated: for each instance the randomly chosen values are drawn anew¹. Apart from the first subgroup, the benchmarks are non-separable. Other specific properties are discussed in Function Properties.

General Setup

Search Space

All functions are defined and can be evaluated over \mathcal{R}^{D}, while the actual search domain is given as [-5,5]^{D}.

Location of the Optimal \mathbf{x}^\mathrm{opt} and of f_\mathrm{opt}=f(\mathbf{x^\mathrm{opt}})

All functions have their global optimum in [-5,5]^{D}. The majority of functions has the global optimum in [-4,4]^{D} and for many of them \mathbf{x}^\mathrm{opt} is drawn uniformly from this compact. The value for f_\mathrm{opt} is drawn from a Cauchy distributed random variable, with zero median and with roughly 50% of the values between -100 and 100. The value is rounded after two decimal places and set to \pm1000 if its absolute value exceeds 1000. In the function definitions a transformed variable vector \mathbf{z} is often used instead of the argument \mathbf{x}. The vector \mathbf{z} has its optimum in \mathbf{z^\mathrm{opt}}=\mathbf{0}, if not stated otherwise.

Boundary Handling

On some functions a penalty boundary handling is applied as given with f^{{}}_\mathrm{pen} (see Symbols and definitions).

Linear Transformations

Linear transformations of the search space are applied to derive non-separable functions from separable ones and to control the conditioning of the function.

*Non-Linear Transformations and Symmetry Breaking

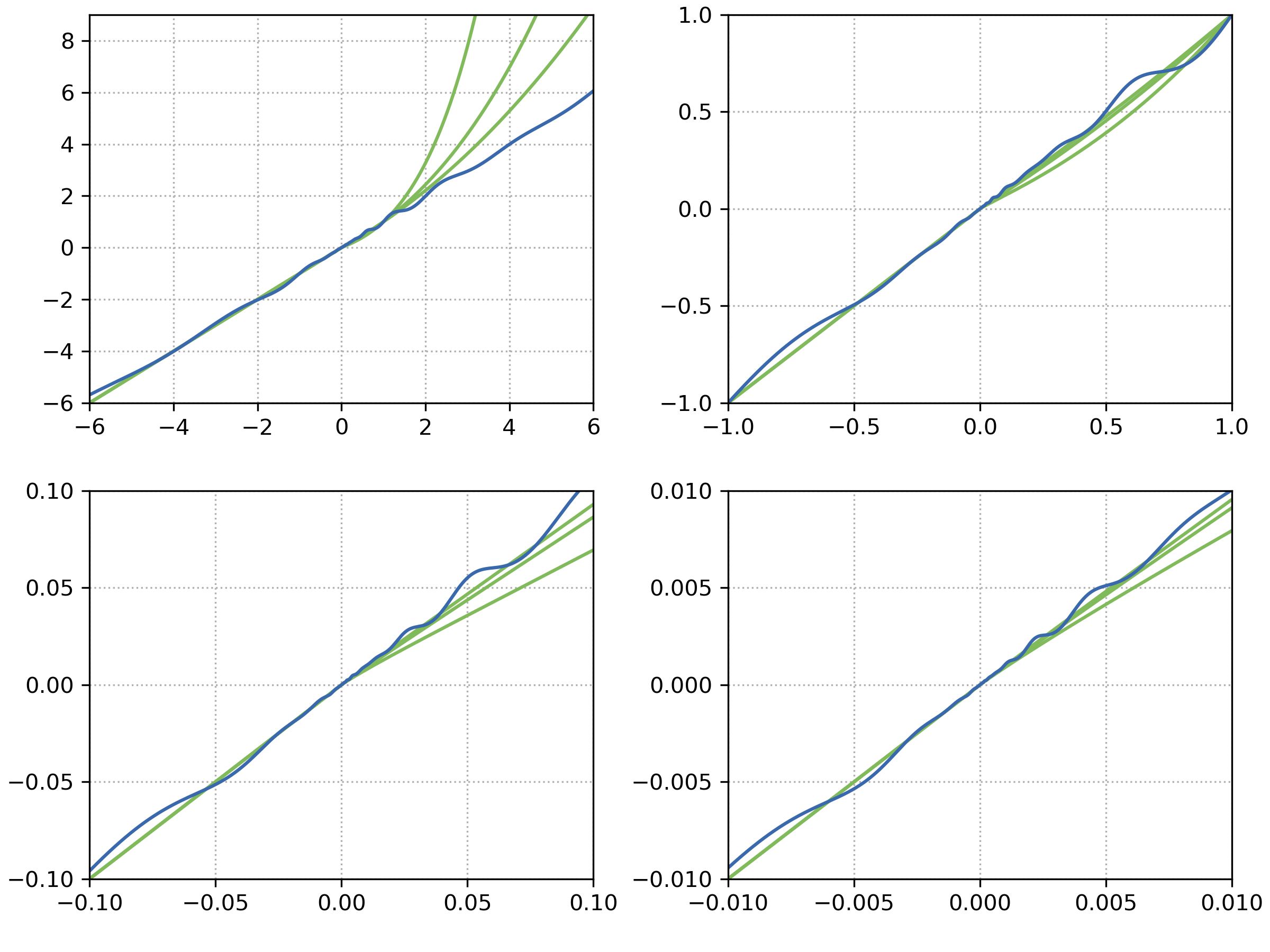
In order to make relatively simple, but well understood functions less regular, on some functions non-linear transformations are applied in x- or f-space. Both transformations T_\mathrm{\hspace*{-0.01emosz}}:\mathcal{R}^n\to\mathcal{R}^n, n\in\{1,D\}, and T_\mathrm{asy}:\mathcal{R}^D\to\mathcal{R}^D are defined coordinate-wise (see Symbols and definitions). They are smooth and have, coordinate-wise, a strictly positive derivative. They are shown in Figure 1. T_\mathrm{osz} is oscillating about the identity, where the oscillation is scale invariant w.r.t. the origin. T^{{}}_\mathrm{asy} is the identity for negative values. When T^{{}}_\mathrm{asy} is applied, a portion of 1/2^D of the search space remains untransformed.

Figure 1: T_\mathrm{osz} (blue) and D-th coordinate of T_\mathrm{asy} for \beta = 0.1, 0.2, 0.5 (green)

Symbols and Definitions

Used symbols and definitions of, e.g., auxiliary functions are given in the following. Vectors are typeset in bold and refer to column vectors.

\otimes indicates element-wise multiplication of two D-dimensional vectors, \otimes:\mathcal{R}^D\times\mathcal{R}^D\to\mathcal{R}^D, (\mathbf{x},\mathbf{y})\mapsto\mathrm{{diag}}(\mathbf{x})\times\mathbf{y}=(x_i\times y_i)_{i=1,\dots,D}

\|.\| denotes the Euclidean norm, \|\mathbf{x}\|^2=\sum_i x_i^2.

[.] denotes the nearest integer value

\mathbf{0} =(0,\dots,0)^{\mathrm{T}} all zero vector

\mathbf{1} =(1,\dots,1)^{\mathrm{T}} all one vector

\Lambda^{\!\alpha} is a diagonal matrix in D dimensions with the ith diagonal element as \lambda_{ii} = \alpha^{\frac{1}{2}\frac{i-1}{D-1}}, for i=1,\dots,D.

f^{{}}_\mathrm{pen} :\mathcal{R}^D\to\mathcal{R}, \mathbf{x}\mapsto\sum_{i=1}^D\max(0,|x_i| - 5)^2

\mathbf{1}_-^+ a D-dimensional vector with entries of -1 or 1 with equal probability independently drawn.

\mathbf{Q}, \mathbf{R} orthogonal (rotation) matrices. For one function in one dimension a different realization for respectively \mathbf{Q} and \mathbf{R} is used for each instantiation of the function. Orthogonal matrices are generated from standard normally distributed entries by Gram-Schmidt orthonormalization. Columns and rows of an orthogonal matrix form an orthonormal basis.

\mathbf{R} see \mathbf{Q}

T^{{\beta}}_\mathrm{asy} :\mathcal{R}^D\to\mathcal{R}^D, x_i\mapsto \begin{cases} x_i^{1+\beta \frac{i-1}{D-1}\sqrt{x_i}} & \text{~if~} x_i>0\\ x_i & \text{~otherwise~} \end{cases}, for i=1,\dots,D. See Figure 1.

T_\mathrm{\hspace*{-0.01em}osz} :\mathcal{R}^n\to\mathcal{R}^n, for any positive integer n (n=1 and n=D are used in the following), maps element-wise x\mapsto\mathrm{{sign}}(x)\exp\left(\hat{x} + 0.049\left(\sin(c_1 \hat{x}) + \sin(c_2 \hat{x})\right)\right) with \hat{x}= \begin{cases} \log(|x|) & \text{if~} x\not=0 \\ 0 & \text{otherwise} \end{cases}, \mathrm{{sign}}(x) = \begin{cases} -1 & \text{if~} x < 0 \\ 0 & \text{if~} x = 0 \\ 1 & \text{otherwise} \end{cases}, c_1 = \begin{cases} 10 & \text{if~} x > 0\\ 5.5 & \text{otherwise} \end{cases} and c_2 = \begin{cases} 7.9 & \text{if~} x > 0\\ 3.1 & \text{otherwise} \end{cases}. See Figure 1.

\mathbf{x}^\mathrm{opt} optimal solution vector, such that f(\mathbf{x^\mathrm{opt}}) is minimal.

Function properties

Deceptive Functions

All “deceptive” functions provide, beyond their deceptivity, a “structure” that can be exploited to solve them in a reasonable procedure.

Ill-Conditioning

Ill-conditioning is a typical challenge in real-parameter optimization and, besides multimodality, probably the most common one. Conditioning of a function can be rigorously formalized in the case of convex quadratic functions, f({\mathbf{x}}) =\frac12 {\mathbf{x}}^{T} {\mathbf{H}}{\mathbf{x}} where {\mathbf{H}} is a symmetric definite positive matrix, as the condition number of the Hessian matrix {\mathbf{H}}. Since contour lines associated to a convex quadratic function are ellipsoids, the condition number corresponds to the square root of the ratio between the largest axis of the ellipsoid and the shortest axis. For more general functions, conditioning loosely refers to the square of the ratio between the largest direction and smallest of a contour line. The testbed contains ill-conditioned functions with a typical conditioning of 10^6. We believe this a realistic requirement, while we have seen practical problems with conditioning as large as 10^{10}.

Regularity

Functions from simple formulas are often highly regular. We have used a non-linear transformation, T_\mathrm{\hspace*{-0.01em}osz}, in order to introduce small, smooth but clearly visible irregularities. Furthermore, the testbed contains a few highly irregular functions.

Separability

In general, separable functions pose an essentially different search problem to solve, because the search process can be reduced to D one-dimensional search procedures. Consequently, non-separable problems must be considered much more difficult and most benchmark functions are designed being non-separable. The typical well-established technique to generate non-separable functions from separable ones is the application of a rotation matrix \mathcal{R}.

Symmetry

Stochastic search procedures often rely on Gaussian distributions to generate new solutions and it has been argued that symmetric benchmark functions could be in favor of these operators. To avoid a bias in favor of highly symmetric operators we have used a symmetry breaking transformation, T^{{}}_\mathrm{asy}. We have also included some highly asymmetric functions.

Target function value to reach

The typical target function value for all functions is {f_\mathrm{opt}}+{10^{-8}}. On many functions a value of {f_\mathrm{opt}}+1 is not very difficult to reach, but the difficulty versus function value is not uniform for all functions. These properties are not intrinsic, that is {f_\mathrm{opt}}+{10^{-8}} is not intrinsically “very good”. The value mainly reflects a scalar multiplier in the function definition.

References

Finck, S., Hansen, N., Ros, R., and Auger, A. (2009), Real-parameter black-box optimization benchmarking 2009: Noiseless functions definitions, INRIA.

Hansen, N., Auger, A., Brockhoff, D., and Tušar, T. and (2022), “Anytime performance assessment in blackbox optimization benchmarking,” IEEE Transactions on Evolutionary Computation, IEEE, 26, 1293–1305.

Hansen, N., Auger, A., Finck, S., and Ros, R. (2009), Real-parameter black-box optimization benchmarking 2009: Experimental setup, INRIA.

Hansen, N., Tušar, T., Mersmann, O., Auger, A., and Brockhoff, D. (2016), “COCO: The experimental procedure,” arXiv preprint arXiv:1603.08776.

Footnotes

The implementation provides an instance ID as input, such that a set of uniquely specified instances can be explicitly chosen.↩︎

Separable

Low or moderate conditioning

High conditioning and unimodal

Multi-modal with adequate global structure

Multi-modal with weak global structure